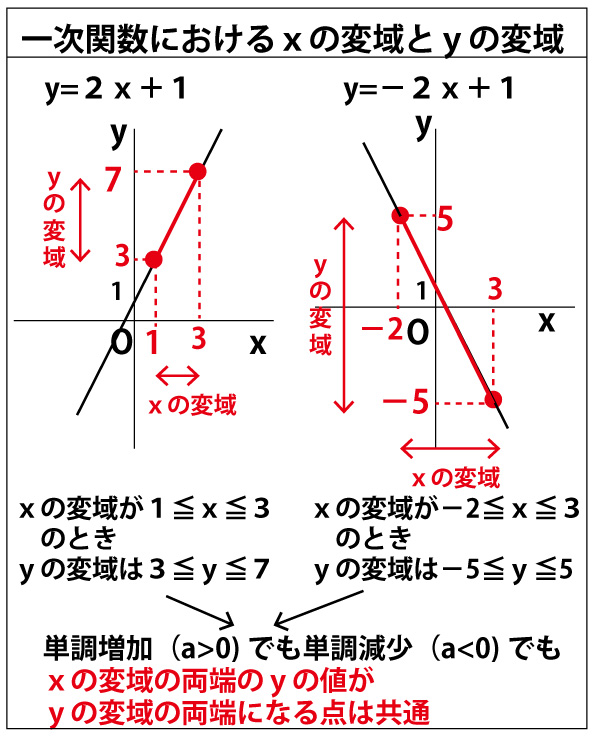
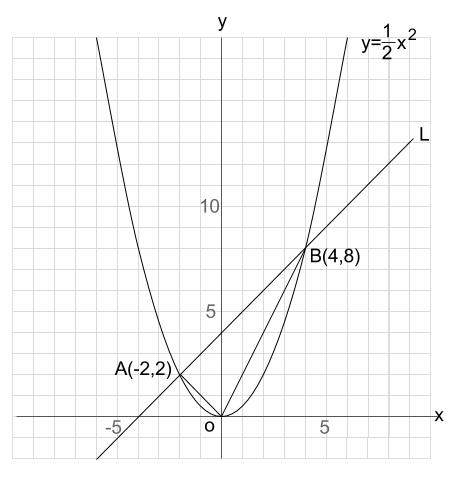
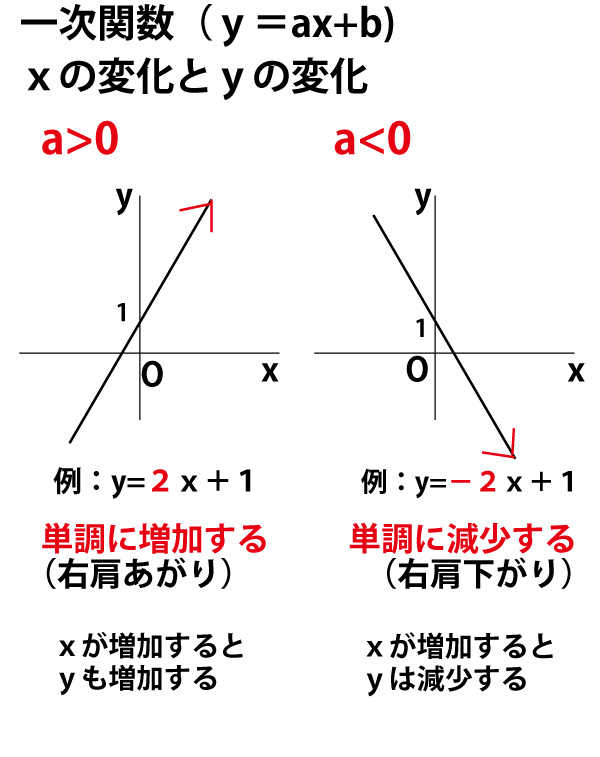
関数 について、 の値が2から4まで増加するときの変化の割合を求めなさい。 変化している の値に注目して、それらの値を足します。 そして、この値に比例定数を掛けます。 今回の問題であれば2ですね。 という感じで、一瞬で計算することができます
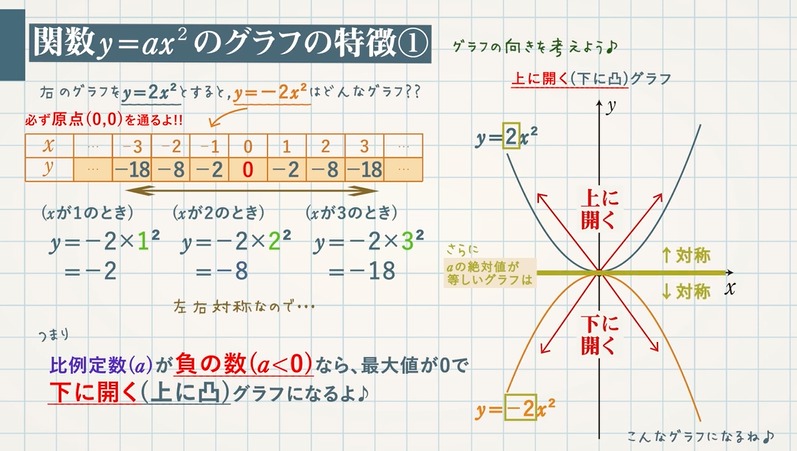
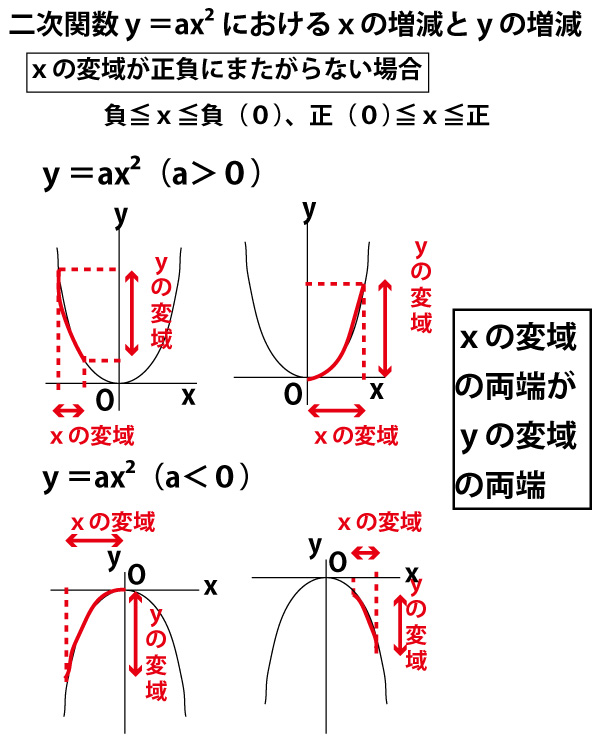
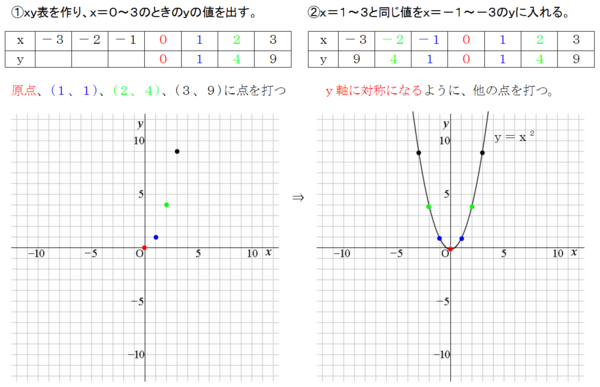
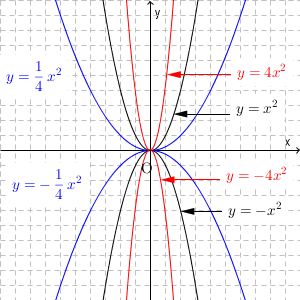
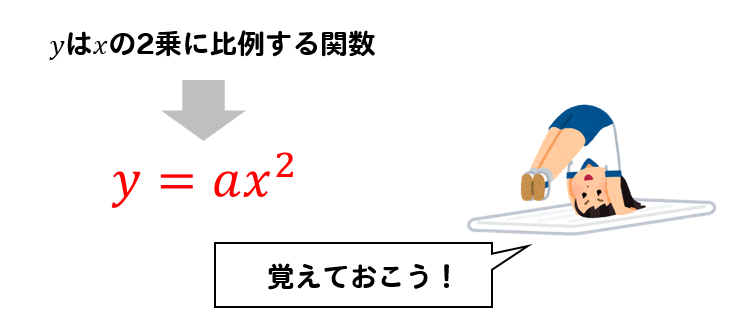
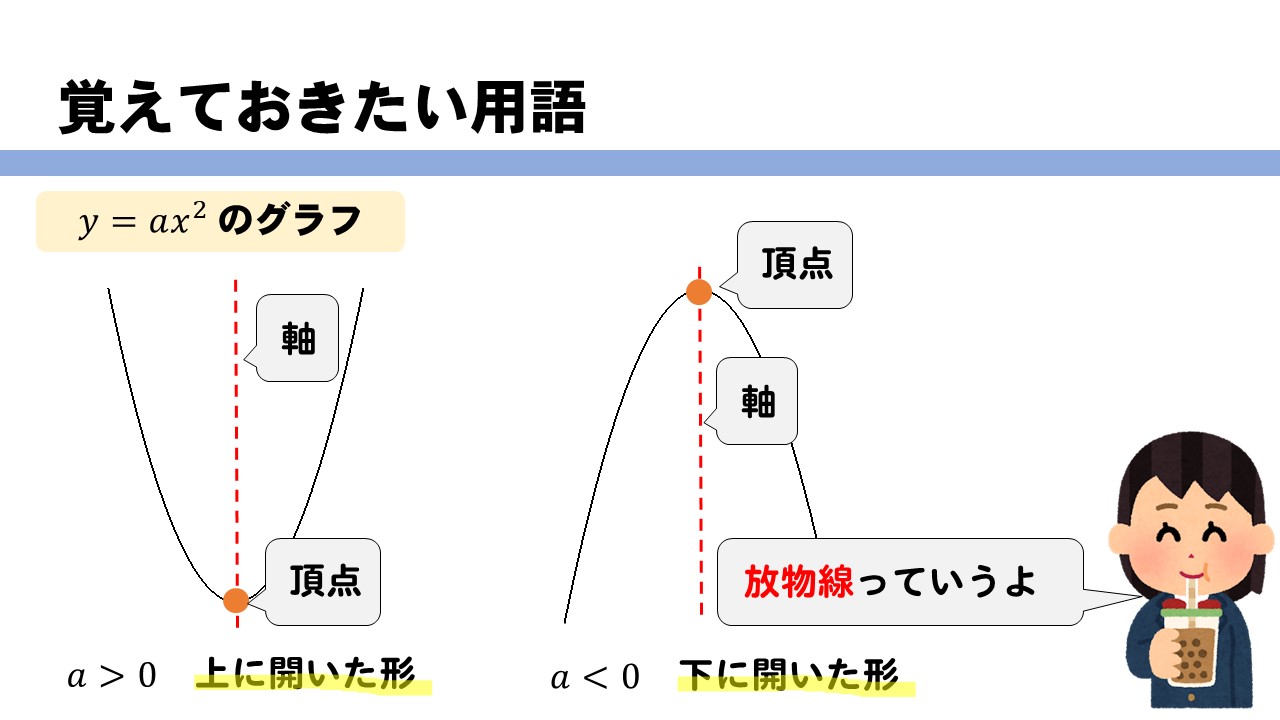
関数y=ax2乗 グラフ-今回の動画では中学3年生で習う数学 二次関数 y=ax2乗の変域の基礎、基本ついて学びましょう!#二次関数 #変域 #二乗#二次関数 #二乗 #関数 今回の動画では中学3年生で習う数学 二次関数より y=ax2乗のグラフ (aく0)の基礎、基本ついて学びましょう!
関数y=ax2乗 グラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
 |  | |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 | ||
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「関数y=ax2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
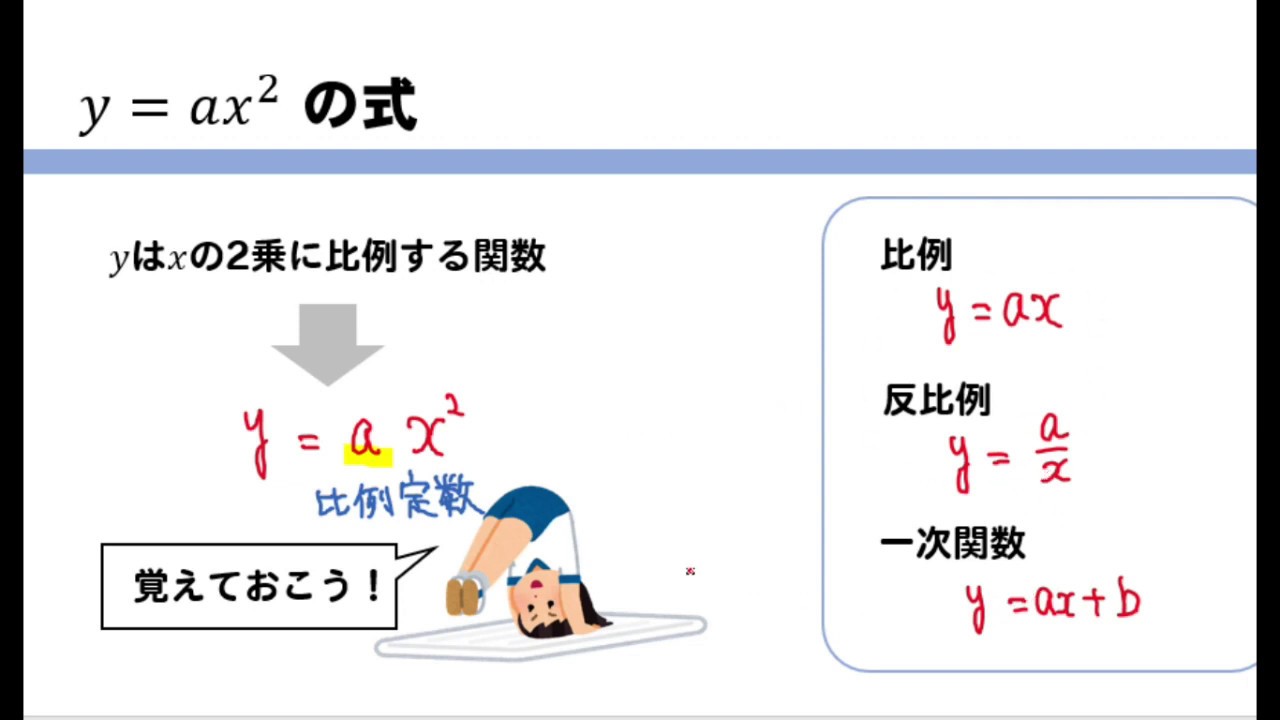
「2乗に比例する関数」 では、 y=ax² の "a" の部分は、 「比例定数」としか呼べない んです。 (直線ではないので、 「傾き」とは呼べないですね。 ) また、 「変化の割合」 についても、 以下の方法で計算すれば、 "a の値"とは違うと分かります。 お悩みは今日で解決できますよ! y=ax² の「変化の割合」の求め方は? では、「変化の割合」について、 求め方(計算法)をお見せします。 「変化概要 この公式の名前は、18世紀の数学者レオンハルト・オイラーに因むが、最初の発見者はロジャー・コーツとされる。 コーツは1714年に () = を発見した が、三角関数の周期性による対数関数の多価性を見逃した。 1740年頃、オイラーは、コーツの公式を基に、指数関数と三角関数の級数展開
Incoming Term: 関数y=ax2乗, 関数y=ax2乗 グラフ, 関数y=ax2乗 変域, 関数y=ax2乗 変化の割合, 関数y=ax2乗 問題, 関数y=ax2乗 応用問題, 関数y=ax2乗 aの値, 関数y=ax2乗 まとめ, 関数y=ax2乗 変域 応用, 関数y=ax2乗 直線の式,




0 件のコメント:
コメントを投稿