1 次 関数 解き方 195519-１次関数 解き方

一次関数には傾きと切片があり、 y = a x b の式になる 比例の公式は y = a x です。 一方で一次関数の公式は y = a x b となります。 特定のポイントからスタートするため、比例の公式に対して b を加えます。 b は x = 0 のときの値です。 先ほどの例であれば、既に5000円の貯金がありました。 そのため、 b = 5000 となります。 一次関数では、 y = a x b の a を傾きとそれぞれの1次関数でxの変域が( )内のときのyの変域を求めよ。 1次関数 要点 1次関数とは 1次関数 変化の割合 1次関数 式の出し方 1次関数 連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明 教科書 新編 新しい数学2 東京書籍, 単元 1次関数, 「解き方を重視したノートを作りました ~ 私自身 ここの単元の 問題の解き方が ごちゃごちゃ になっているので笑 まとめてみました() まだ解き慣れていないだけかもですが笑🥺 ここの単元苦手な人っ一緒に頑張りましょｯｯ ️ と 💬 も

至急お願いします 中２の一次関数の問題なのですが解き方が分かり Yahoo 知恵袋

１次関数 解き方

１次関数 解き方- 中学と高校の数学の解き方のコツ 因数分解の公式 不等式の解き方 二次関数の頂点の座標 絶対値 方程式の解き方 三角関数sin cos tan なるべく図を書いて、右脳で理解するのが数学の解き方のコツです。 公式を言葉だけで覚えないように。1次関数基礎1 1 次の問いに答えよ。 (1)1次関数でxが2から3まで変化したときにyは5から7まで変化した。変化の割合を求めよ。 (2)1次関数でxが3から7まで変化するときにyが2から–6まで変化した。変化の割合を求めよ。 (3)y=–2x3について 変化の割合を求めよ。

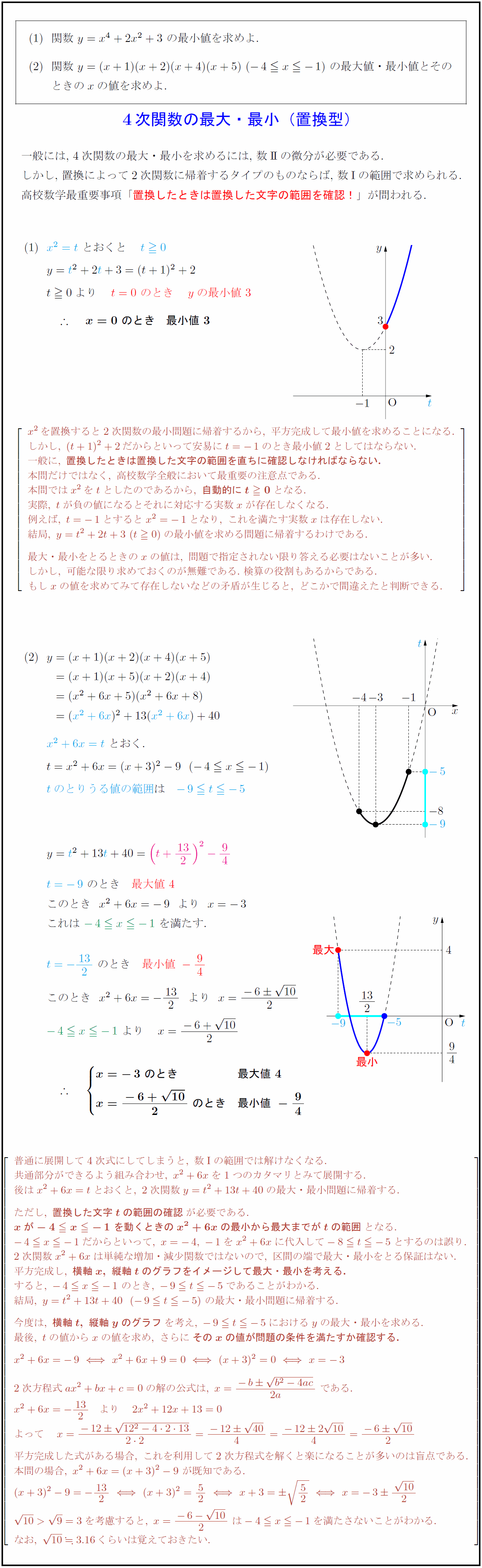
高校数学 4次関数の最大 最小 置換型 受験の月

解き方 まず、軸x=3を求めます。 次に、軸x=3と変域a≦x≦a2の中央値 を比べます。 最大値は 1 a1≦3のとき、つまりa≦2のとき、x=aの方が遠いので f(a)=a²6a5 ※a1=2の場合を個別に解く必要はありません。 （ア） 最大値 aと中央値2の位置で場合分けします。大学受験における1次関数の概要 大学受験の数学において重要な単元の一つが、1次関数。 二次関数を解く際にも、1次関数を利用することもあります。 1次関数の概要としては2つの変数x、yがあるとき、1次関数は次の式で表されます。二次不等式の解き方を簡単に！高校数学をマスターしよう！ 文字係数の2次不等式の解き方！場合分けの考え方は？？ 解からの係数決定！グラフの形と座標に注目せよ！ 絶対不等式！パターン別の例題を使って解き方を解説！ 2次方程式の解の存在範囲！

 一次関数y=axbのグラフの書き方の手順 ①x軸、y軸、原点を書く ②一次関数y=axbは必ず点 (0,b)を通ります (x=0のときy=b)。 y軸上にbの値を記入します。 このときbをy切片と呼びます。 ③もう一点、y=axbが通る点を見つけます。 (s,asb)とします。 (0,b) (s,asb)の二点を結ぶことでy=axbの直線が引けます。 もう一点見つける時は、x=±1、±2あたりを調べると例題 次の 2次関数の頂点の座標と軸の方程式を求めよ。 (1) (2) ① を の形に変形することを、平方完成 といいます。 ② ①の平方完成によって、 2 次関数 の頂点は、 軸は、 と分かります。 ③ 平方完成の手順は、 でくくったあと、 と変形していきます。 平行移動の解き方：その1 1つ目解き方は、平方完成を利用する方法です。 まずは平行移動させたい二次関数を平方完成します。 y=x 24x10を平方完成すると、 y=(x2) 2 6 ですね。 よって、この二次関数の頂点の座標は(2,6)です。

＜キーワードを見つければ ⇒ 決まった解き方が！ ＞ 1 「1次関数」「直線」 とあったら、 ⇒ はじめに 「y＝ax＋b」 と書く。 2 「変化の割合が」「傾きが」 とあったら、 ⇒ 「a」 に数値を代入 「切片が」 とあったら、 ⇒ 「b」 に数値を代入 3見方や考え方 ・1次関数についての基礎的・ 解き方や考え方を説明し合う活動を設定し，考えを広げた り深めたりすると同時に，説明する力を育てる。 ｛第3・4・5・6・7・10・14・16・18時｝ つまり、初めの例題を、「 、 を通る一次関数を求めよ。 」と簡単に言い換えることができたことになります。 この問題の解き方は以前の記事で解説しています。 1次関数1次関数の式の求め方 (2) こんにちは、まぐろです。 今回は、2点を通る一次関数の式の求め方について解説します。 前回の記事と合わせて、一次関数の求め方を確認しておきましょう

Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

次の条件を満たす一次関数の式を求めなさい Clear

 画像の式の第n次導関数の解き方を教えてください。 数学 sin (2x1)のn次導関数を求めてください 数学 f (x)=sin (2x1)の第n次導関数は何ですか？ というか、答えがfⁿ (x)=2ⁿsin (2x−1nπ/2) (n≧0) となっているんですが、なぜそうなるのか分からないので、教え1次関数 f (x) = a x b (a ≠ 0) f(x)=axb\(a\neq 0) f (x) = a x b (a = 0) は全射。 なぜなら，任意の実数 y y y に対して， x = y − b a x=\dfrac{yb}{a} x = a y − b とおけば f (x) = y f(x)=y f (x) = y となる1次関数の式の求め方のコツ について、第一歩を詳しく述べました。 （連立しなくても解ける、 簡単な基本問題を 先にご紹介しています。 そちらの方がより重要だからです。 定期テストの得点アップ法 も 具体的に紹介しました。）

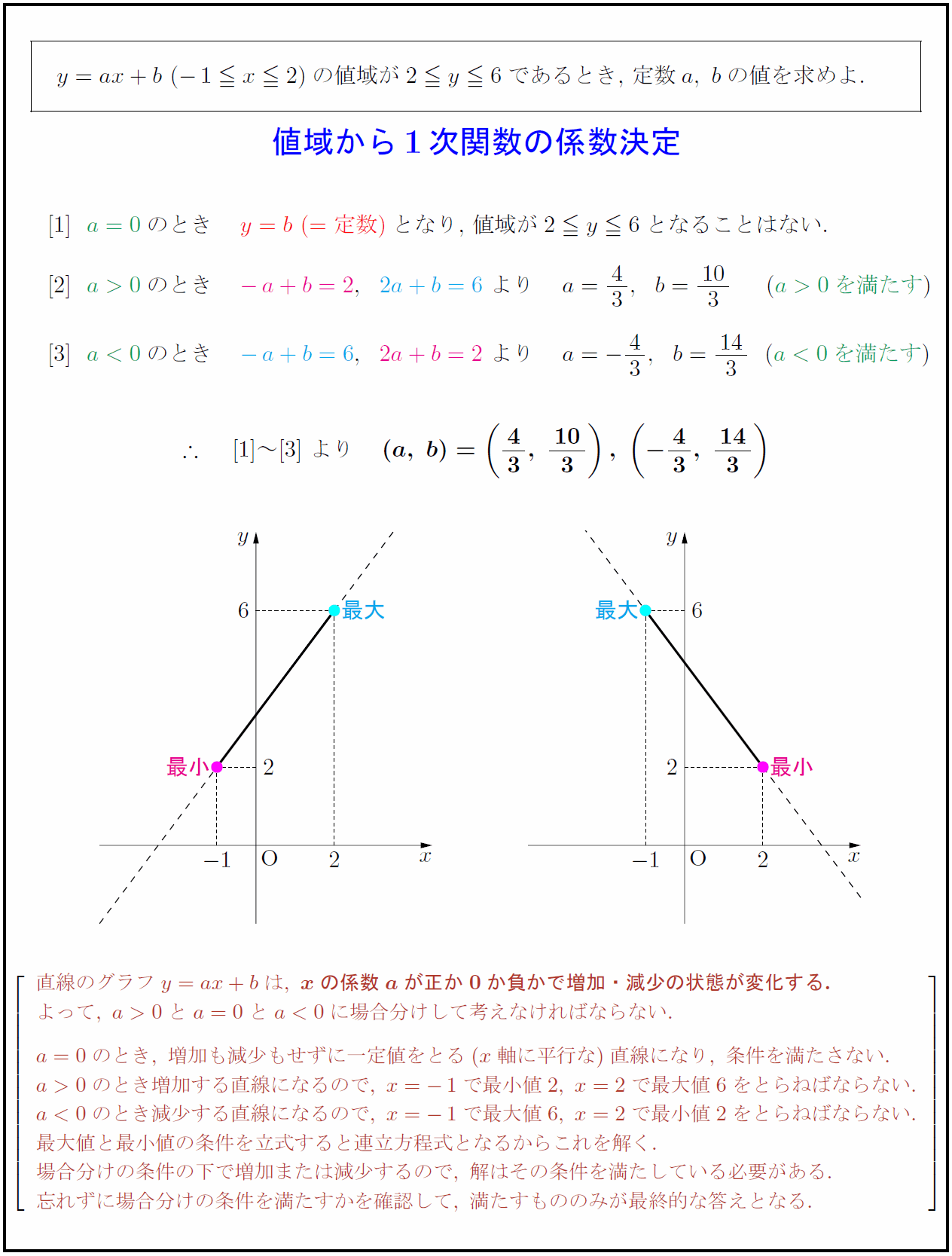
高校数学 値域から1次関数の係数決定 受験の月

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

 二次関数も、一次関数を解くのと同じ感覚で解いていけばいいのです。 二次関数は、例えば「 y=ax2 」と表記します。 a に「 2 」を入れれば「 y=2x2 」になります。 これは、「 y は x の二乗の 2 倍」にすぎません。 先ほどの「 y=2x 」の「 x 」が「 x の二乗」に変わっただけです。 二乗は「同じ数を掛ける」だけなので、難しくありません。 「 y は x の二乗の 2 倍 ここへ到着する 1 次 関数 解き方 ダイアグラムと1次関数 Youtube 一次関数の問題の解き方 7パターン 数学fun 一次関数の利用の問題の解き方 速さ 2 現役塾講師のわかりやすいVideos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer Cancel Confirm Switch camera Share

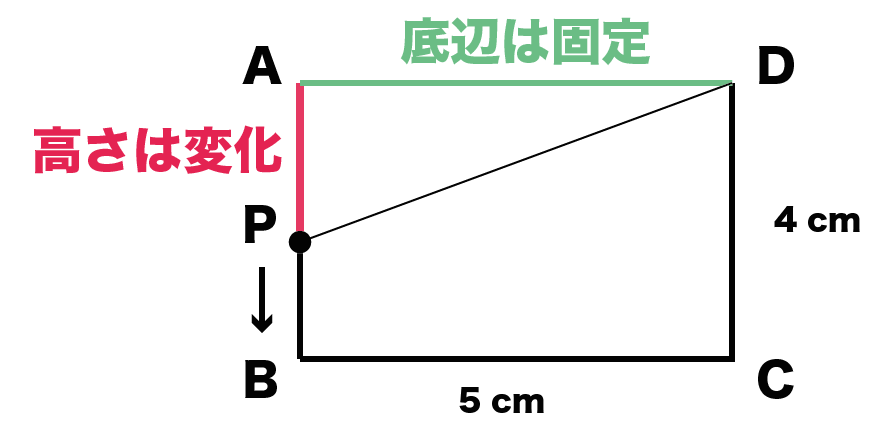
一次関数の利用 動点の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

一次関数 式の求め方をパターン別に問題解説 数スタ

 二次関数の解き方、平方完成、グラフの本質が10分で理解できます！ 二次関数に入ってから数学が嫌いになった！ という声はいつの時代も聞かれて、困ってしまうものです。 高校数学に入ってから初めに難しく感じてしまう二次関数の全体の理論を、10分で理解していただけるように説明したいと思います。 二次関数の章も、教科書とかガン無視で理解重視で行きTap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history 二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 本記事では「二次方程式とは何か」という説明から、3つの解き方の使い分けまでを解説します。 もし、上の3つの二次方程式の解き方を使 55 akk

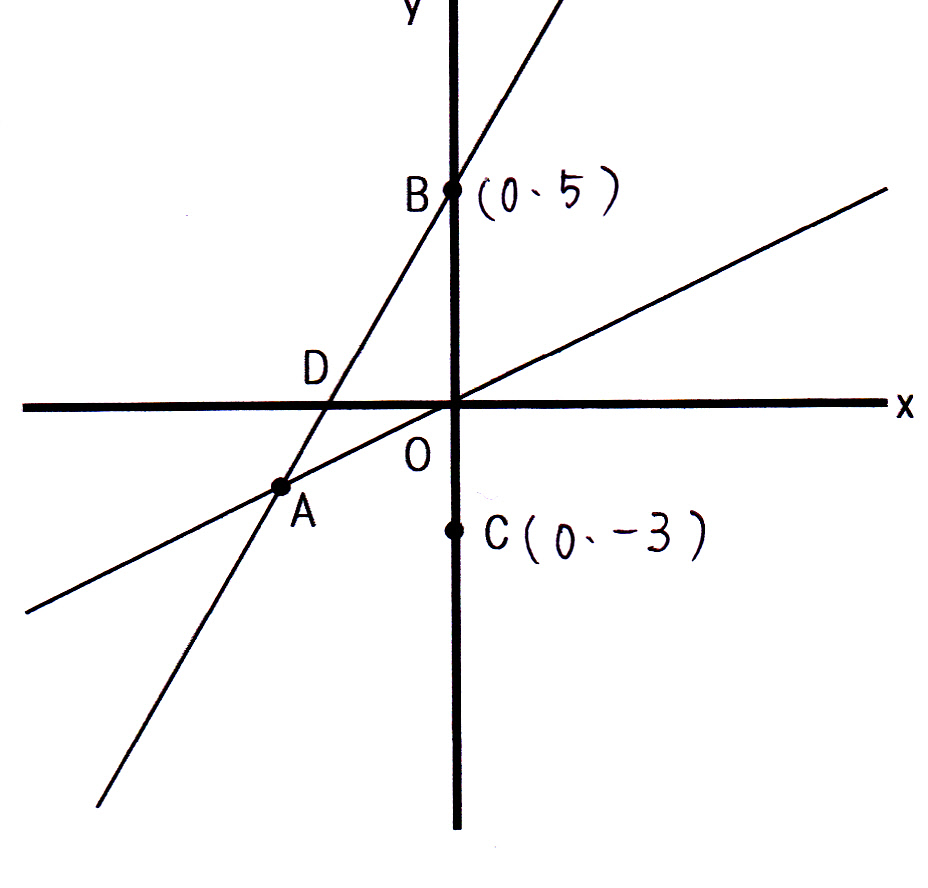
一次関数の利用の問題の解き方 グラフ 3 現役塾講師のわかりやすい中学数学の解き方

一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典

 「yがxの関数で、y＝2x8 、y=5x のように、yがxの一次式で表されるとき、yはxの一次関数であるという」 一次関数は「y=axb, a,b は定数」と表すことができます。つまり、関数y＝（x－α）（x－β）のグラフが x軸より下 になるxの範囲を答えればいいんだ。 y＝（x－α）（x－β） の値がマイナスになる部分、つまりグラフが x軸より下 になる部分を考えると、解は α＜x＜β だね。 「（x－α）（x－β）＜0」 の解は、 「αとβの内側」 というイメージを持とう 一次関数の問題の解き方 パターン1～3文章から一次関数の式を求める パターン4グラフから一次関数の式を求める パターン5与えられた一次関数の式をグラフに書く パターン6\(x\)の変域から\(y\)の変域を求める

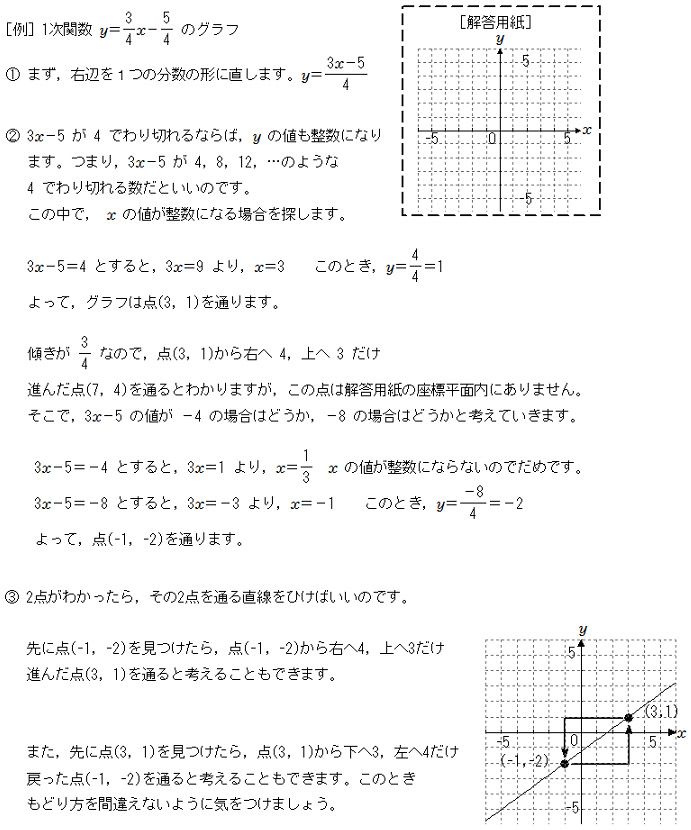
傾きや切片が分数であるグラフのかき方 中学英語 定期テスト対策 ベネッセ教育情報サイト

1次関数 グラフから直線の式を求める 勉強ナビゲーター

一次関数のグラフ書き方まとめ！ 一次関数のグラフから式を求める方法を解説！ 一次関数の式の作り方をパターン別に解説！ 一次関数の座標の求め方は？いろんな座標を求める問題について解説！ 一次関数の増加量に関する問題ってどうやって解く？1次関数(交点の座標の求め方) 更新 交点の座標は，方程式を作って解くだけ 1次関数などの式で表される直線が2本あったとして，その式がそれぞれ，以下の2つだったとします。 では解き方のとおりやってみましょう。 1次関数 変域の求め方 中学数学 定期テスト対策サイト 1 次 関数 解き方 1 次 関数 解き方

高校数学 関数は グラフが命 映像授業のtry It トライイット

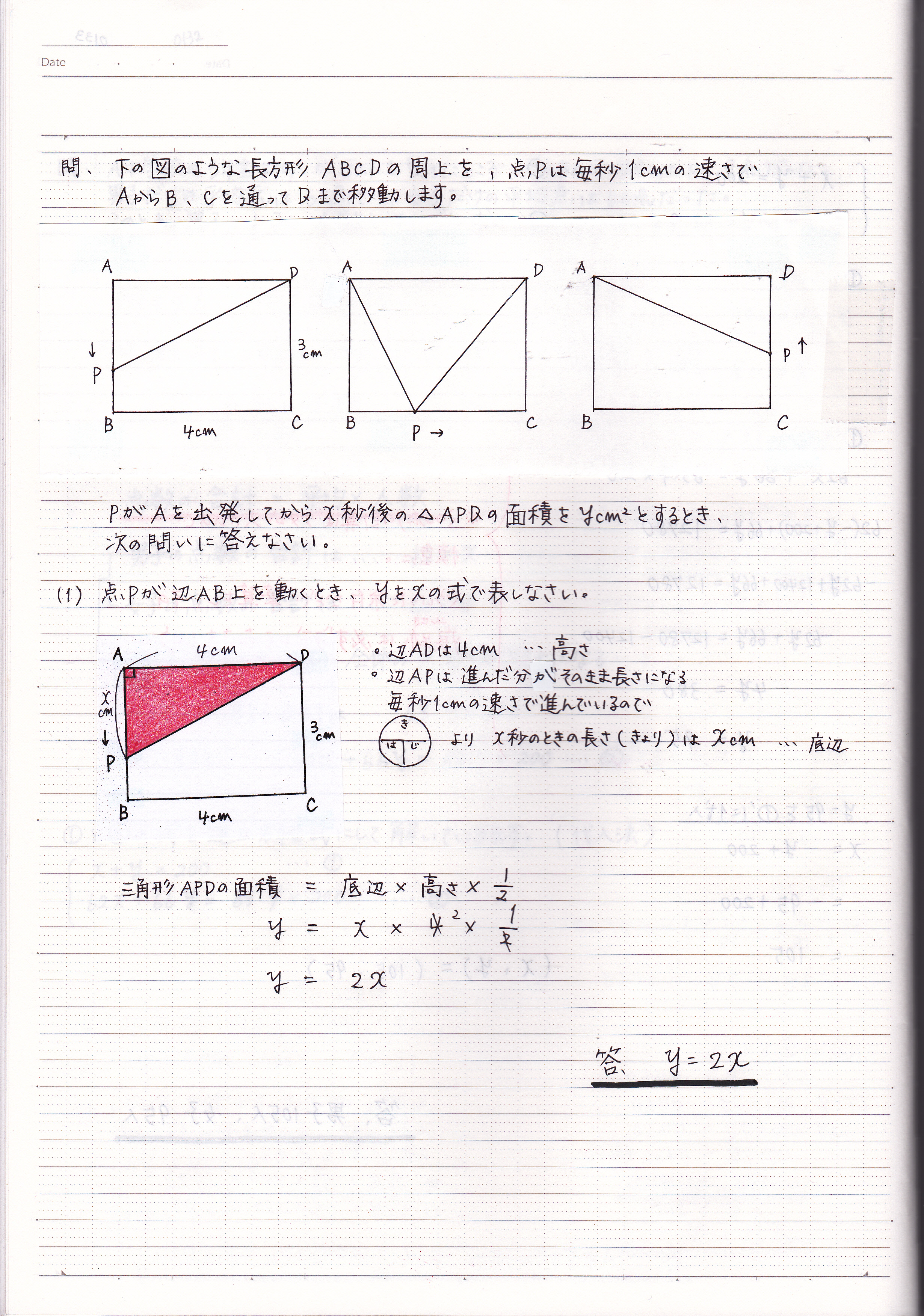
一次関数の利用の問題の解き方 動点 1 現役塾講師のわかりやすい中学数学の解き方

 最も人気のある 1 次 関数 解き方 一次関数の基本問題の解き方 2直線 現役塾講師のわかりやすい中学 一次関数の利用の問題の解き方 速さ 2 現役塾講師のわかりやすい漸化式の発展的な解き方と様々な分野（場合の数，積分，極限，関数方程式）への応用例をまとめました。 漸化式の解き方4：一次の二項間漸化式 関数方程式にまで漸化式が登場。 x = 1 のとき y = 2 − 3 1 = 0 STEP3 f' (x) の符号を調べ、増減表を埋める 符号を調べるときは、適当な x の値を代入してみます。 x = −1 のとき y' = 6 (−1) (−1 − 1) = 12 > 0 \displaystyle x = \frac {1} {2} のとき \displaystyle y' = 6 \left ( \frac {1} {2} \right) \left ( \frac {1} {2} − 1 \right) = −\frac {3} {2} < 0 x = 2 のとき y' = 6 \cdot 2 (2 − 1) = 12 > 0

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

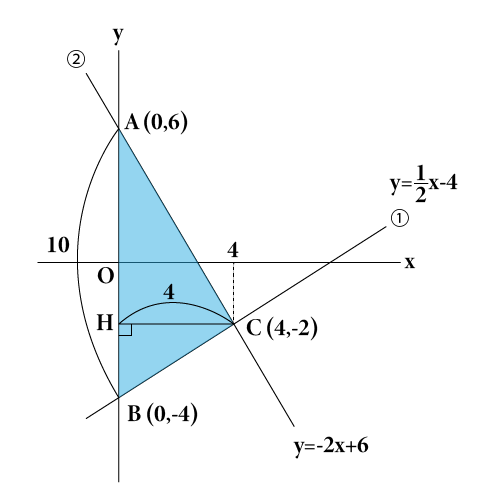
中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾

一次関数で表された図形の面積とは？ 一次関数はグラフに表したときに直線となります。この一次関数が複数あると考えると、直線同士の交点や座標を使って図形が出来ることがあります。 解く方針としては、 直線の式を求める(直線の式が分からない場合)

ダイアグラムと１次関数 Youtube

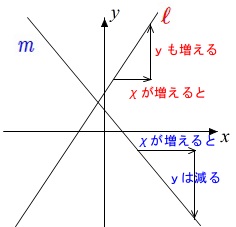
1次関数とは 傾きや切片 変域などの用語と関数の増加減少

例題2の 4 の解き方 グラフへ書くための を教えてください 他のと Yahoo 知恵袋

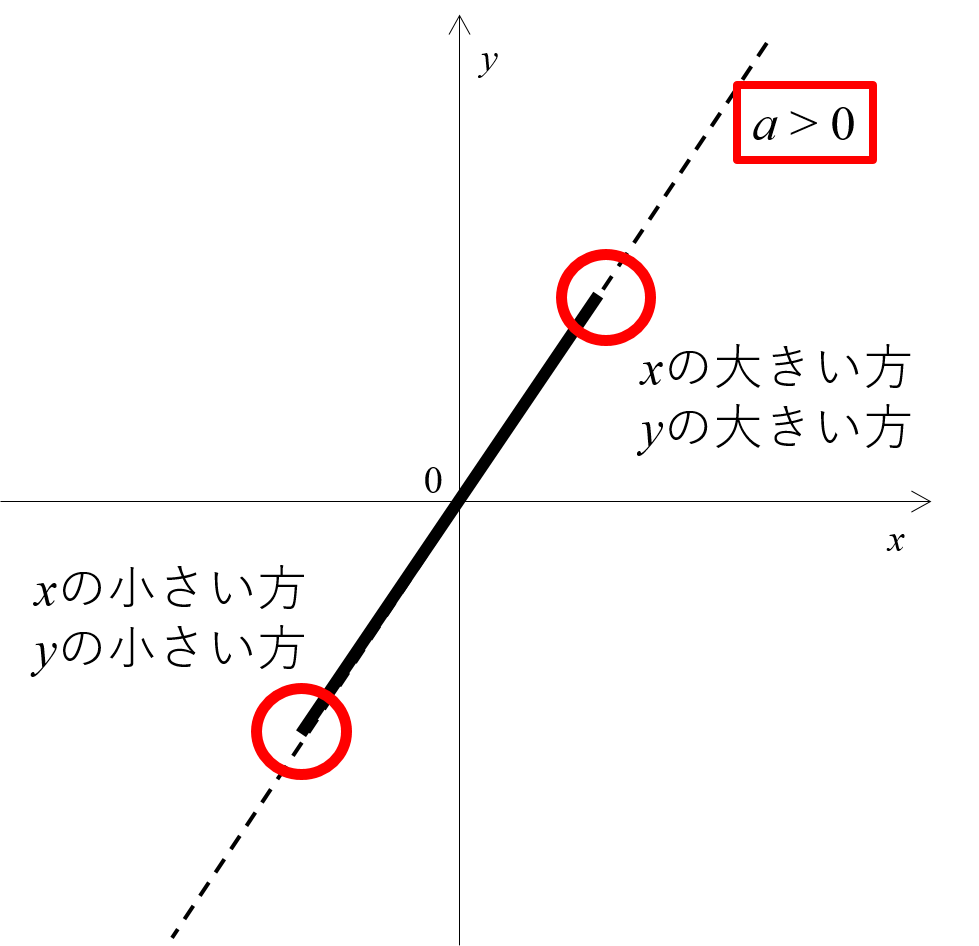
1次関数 変域を使った問題の解き方2 数学がわかるブログ

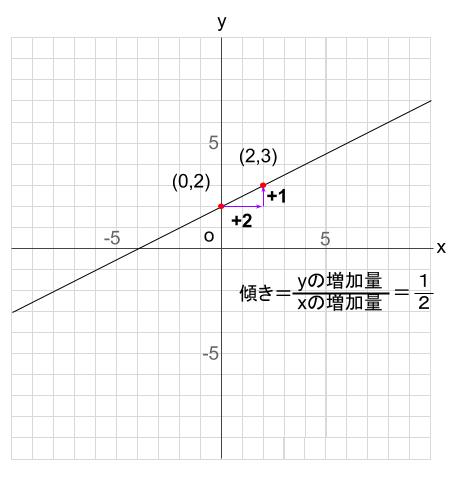
中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su

一次関数の利用の解き方のコツ教えてください Clear

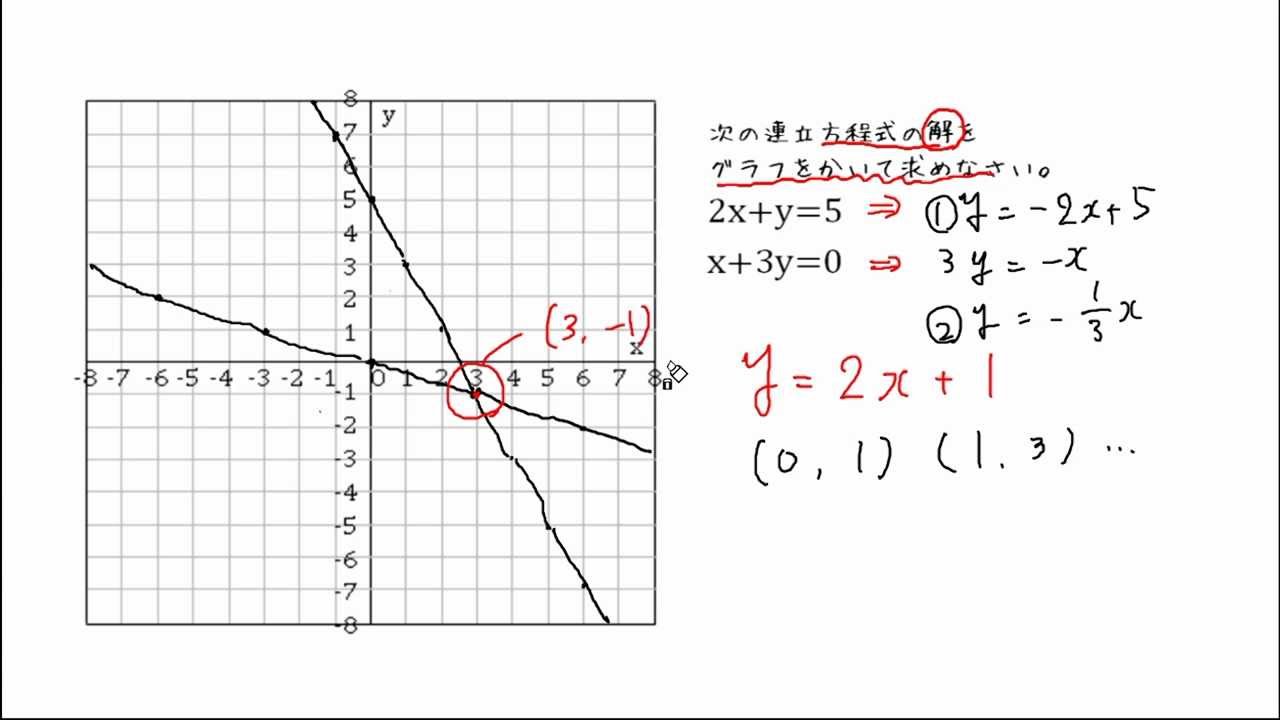
一次関数と連立方程式 Youtube

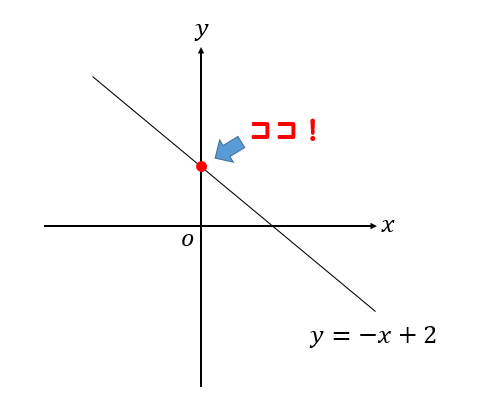
一次関数 座標の求め方は いろんな座標を求める問題について解説 数スタ

完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト

中学２年生 数学 １次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

2

1

一次 関数 問題 解き方

2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun

2

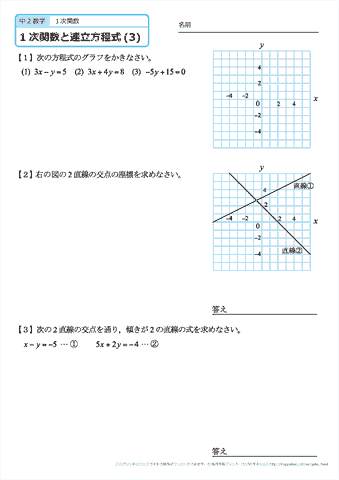
中学２年生 数学 １次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月

１次関数 1次関数の式の求め方 中学数学 定期テスト対策サイト

一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学

次の条件を満たす一次関数の式を求めなさい Clear

2次方程式と2次関数 数学i フリー教材開発コミュニティ Ftext

中学２年生 数学 １次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 このページの問題プリント 全部

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

3

一次関数を子供に教える

0以上 1 次 関数 解き方 シモネタ

数学 中2 44 一次関数の利用 動点編 Youtube

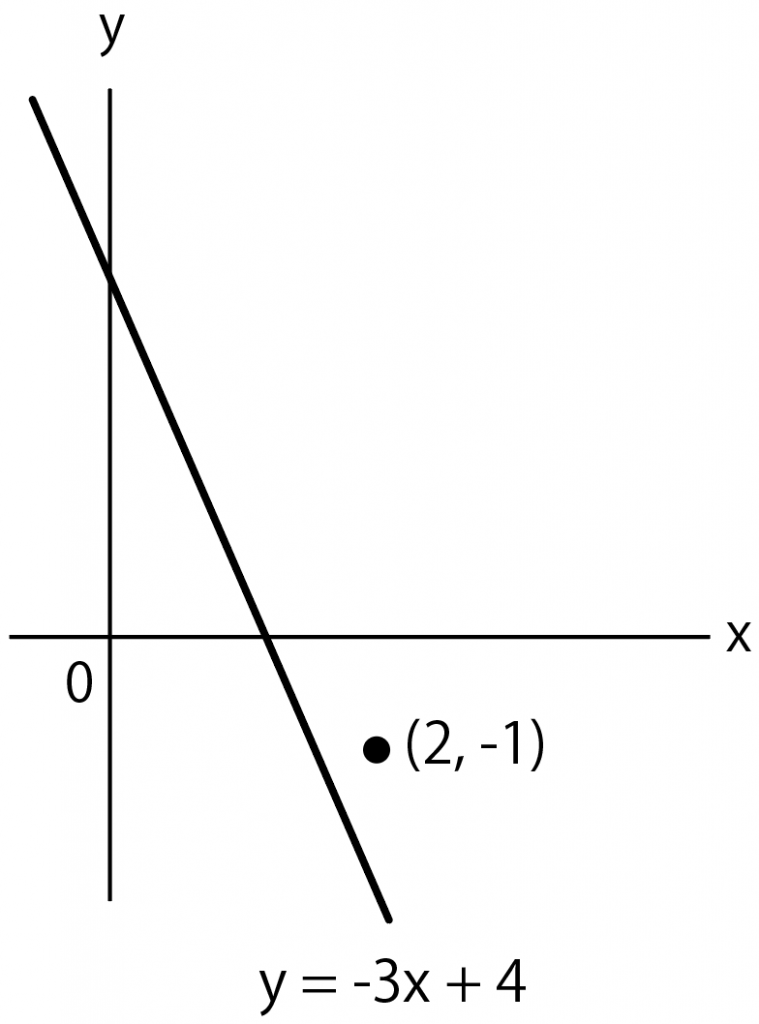
一次関数 テストに出やすい 平行な直線の式の求め方 Qikeru 学びを楽しくわかりやすく

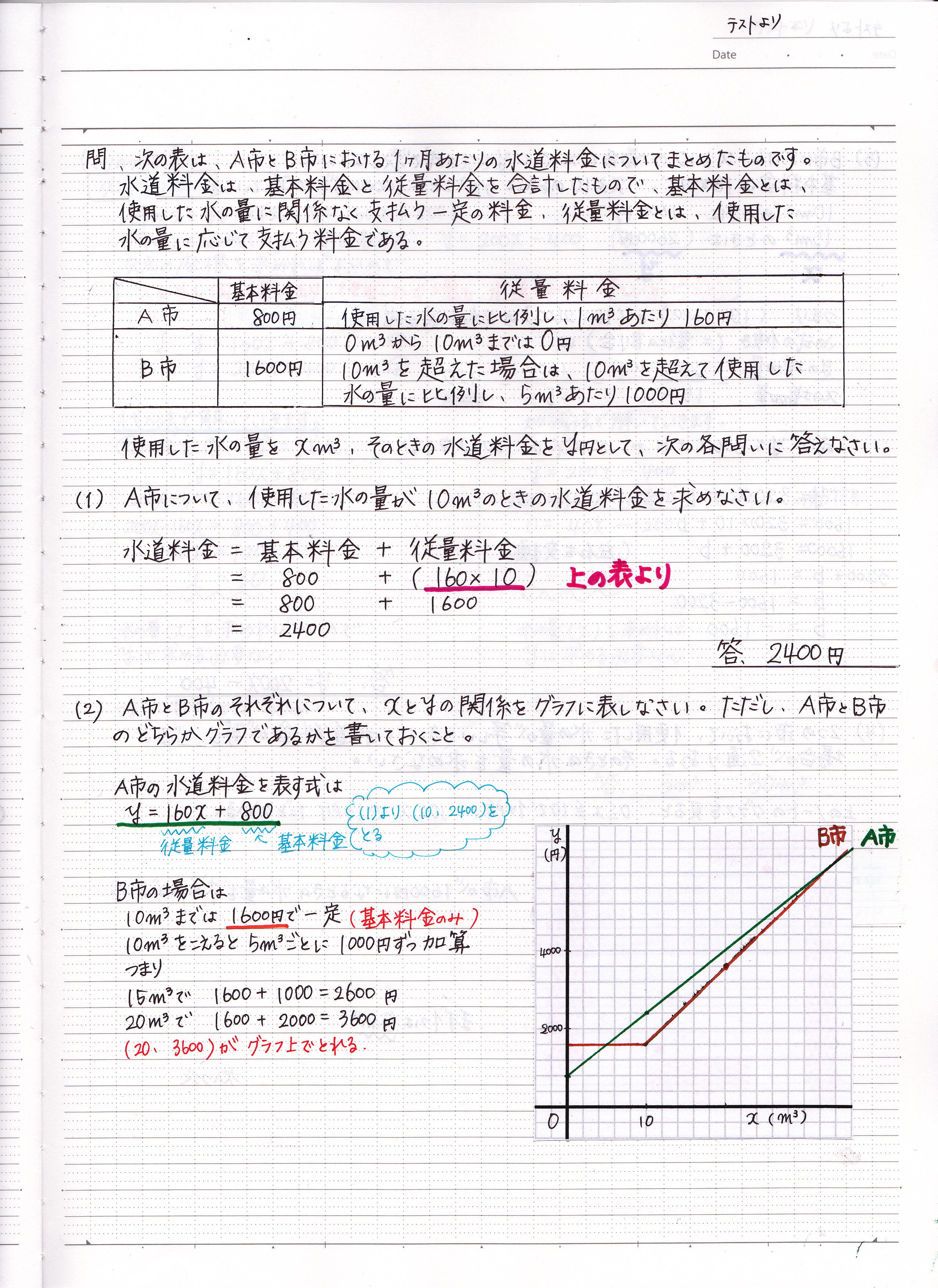
一次関数の利用の問題の解き方 料金 1 現役塾講師のわかりやすい中学数学の解き方

一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス

一次関数写真の解き方を教えてください 1 Y Ax Bの公式に傾き1 Yahoo 知恵袋

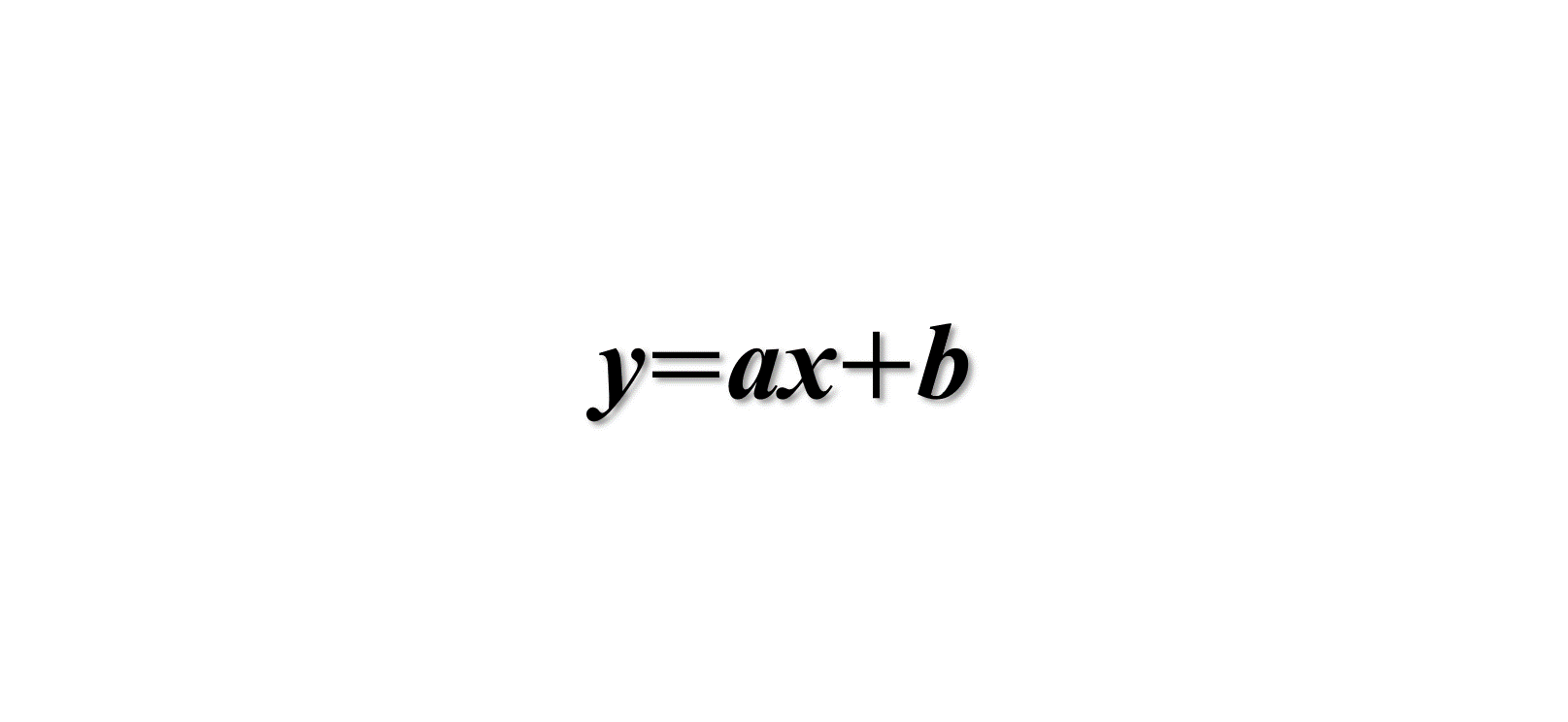
1次関数 変域を使った問題の解き方 数学がわかるブログ

一次関数の問題です Clear

受験 定期試験 数学解き方集 裏技 解法 １次関数の裏ワザの演習 中学数学

一次関数の基本問題の解き方 2直線 現役塾講師のわかりやすい中学数学の解き方

数学 中2 36 一次関数の交点をだす 基本編 Youtube

1次関数のグラフ4

数学 中2 32 一次関数の式をもとめる 基本編 Youtube

至急お願いします 中２の一次関数の問題なのですが解き方が分かり Yahoo 知恵袋

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

一次関数の利用の問題の解き方 速さ 1 2 現役塾講師のわかりやすい中学数学の解き方

高校数学 4次関数の最大 最小 置換型 受験の月

一次関数の利用の問題の解き方 速さ 3 現役塾講師のわかりやすい中学数学の解き方

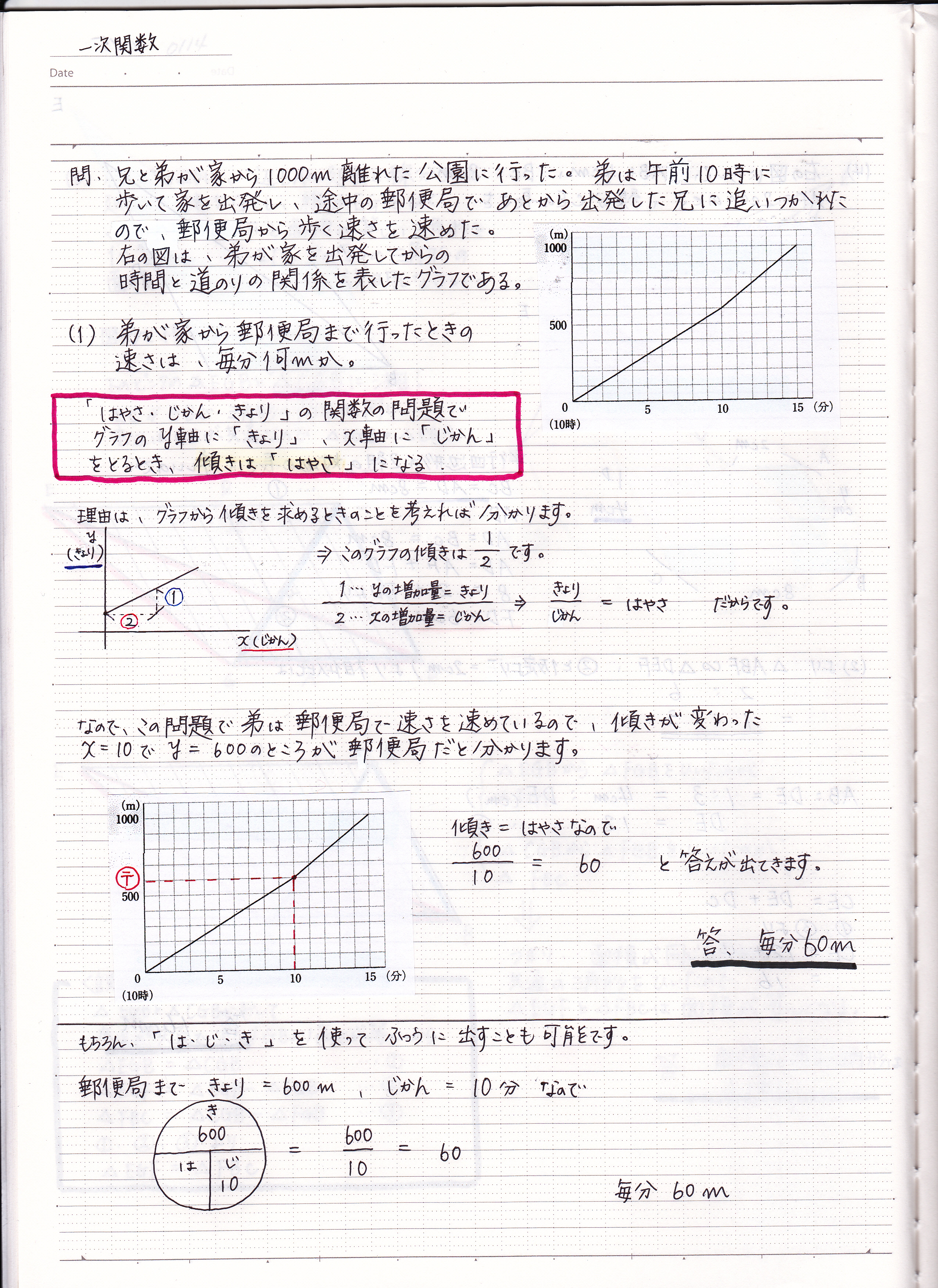
一次関数の利用の問題の解き方 速さ 2 現役塾講師のわかりやすい中学数学の解き方

一次関数の利用の問題の解き方 グラフ 1 現役塾講師のわかりやすい中学数学の解き方

数学 中2 42 一次関数の利用 一人のみはじ編 Youtube

高校数学 放物線と直線との共有点の求め方 映像授業のtry It トライイット

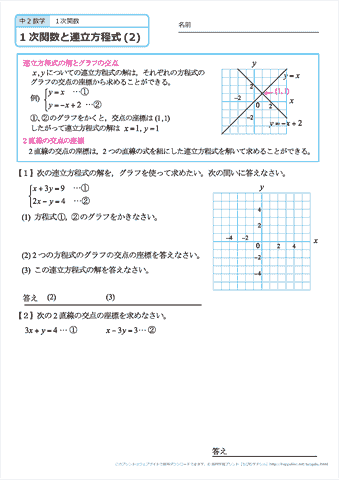
中学２年生 数学 １次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学2年生の数学 1次関数と正方形 長方形 塾講師が数学をやりmath

一次関数の応用問題の解き方がわかりません 弟の数学の宿題を手伝っ 数学 教えて Goo

高校数学 １次不等式とグラフの関係 練習編 映像授業のtry It トライイット

一次関数の問題の解き方 7パターン 数学fun

2

数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube

漸化式にnの１次関数が含まれるときの解き方と別解 例題５

受験 定期試験 数学解き方集 裏技 解法 １次関数の計算テクニック 中学数学

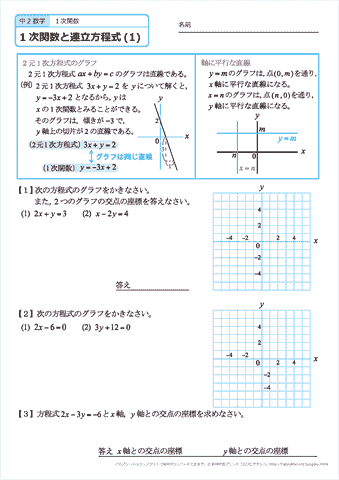
中学２年生 数学 １次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学

一次関数の利用 グラフの意味を考える 苦手な数学を簡単に

中2 1次関数のグラフです Clear

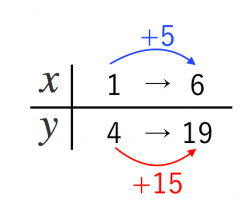
一次関数 文章から式を答える ２種類の解法 苦手な数学を簡単に

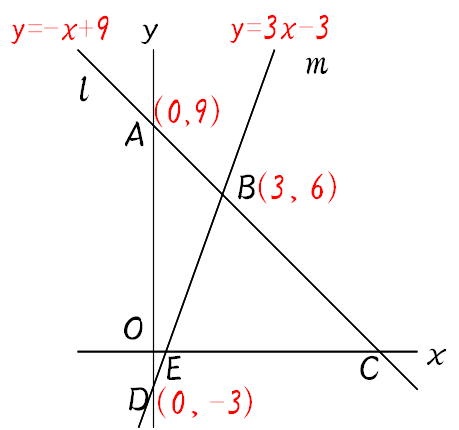
Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

1次関数の変域の求め方 勉強ナビゲーター

一次関数のグラフの利用１ 無料で使える中学学習プリント

一次関数のグラフ 1 2年の復習 です 3 の解き方を教えていただきたいです Clear

一次関数 変域問題の解き方 変域から式を求める方法とは 数スタ

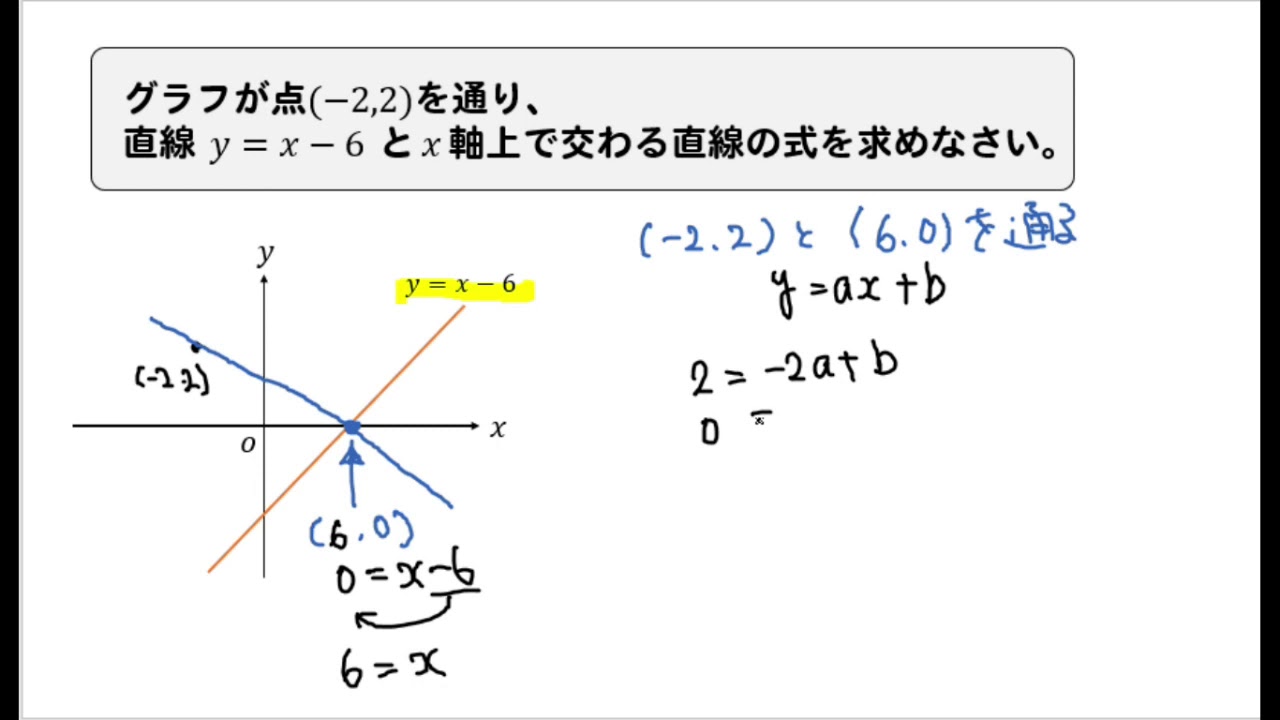
一次関数 X軸上で交わる直線の式の求め方を解説 数スタ

Q Tbn And9gcqnuh1r4e01c3kq3b1f29b Its4bs2jvt Qdbpqyxxkqfrhvrv5 Usqp Cau

中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト

一次関数の利用この問題の解き方がわかりません 式の作り方をわかりやすく Yahoo 知恵袋

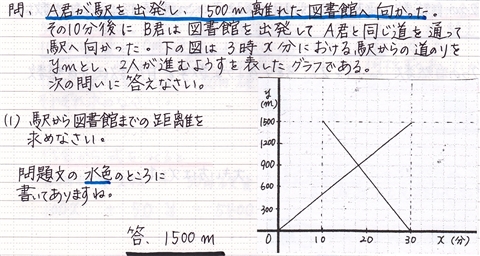
中学の一次関数 ２次関数の勉強のコツを知って得意になろう

一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス

一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく

中2数学一次関数 この問題の解き方が分かりません X座標 Yahoo 知恵袋

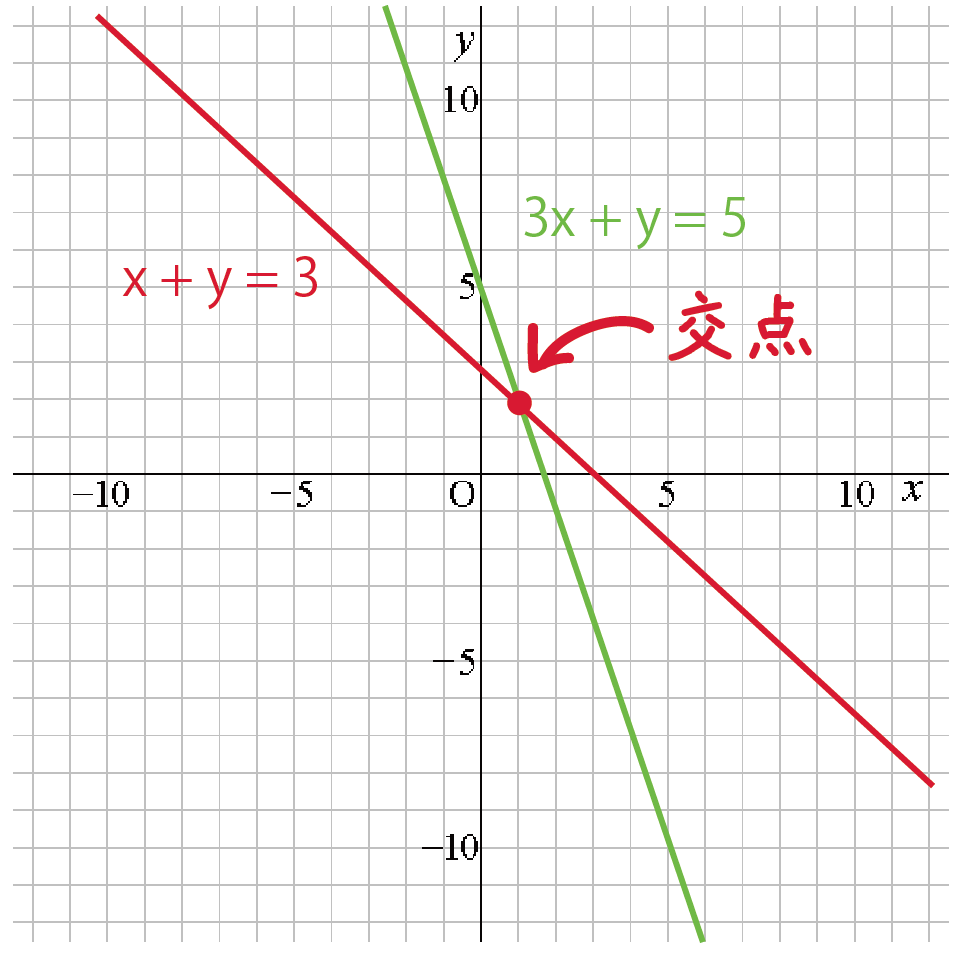
一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく

1

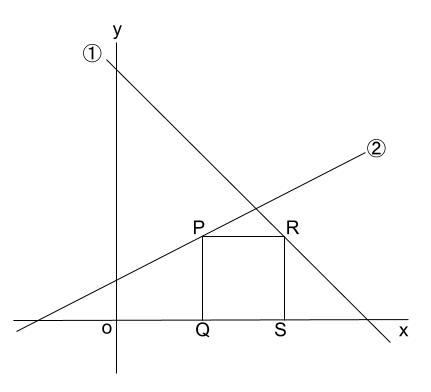
1次関数と正方形 中学数学の無料オンライン学習サイトchu Su

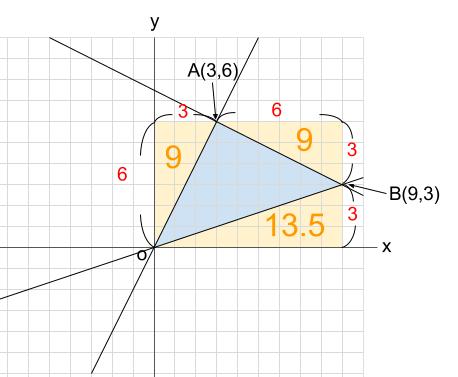
中学数学 １次関数と三角形の面積 その２ 中学数学の無料オンライン学習サイトchu Su

中２数学 きょうの１題 １次関数 ７ 2 中学数学高校数学個別指導in山形市 数専ゼミ

一次関数 グラフの書き方 切片が分数のときにはどうする Youtube

Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

一次関数とは 式とグラフの解説 数学fun

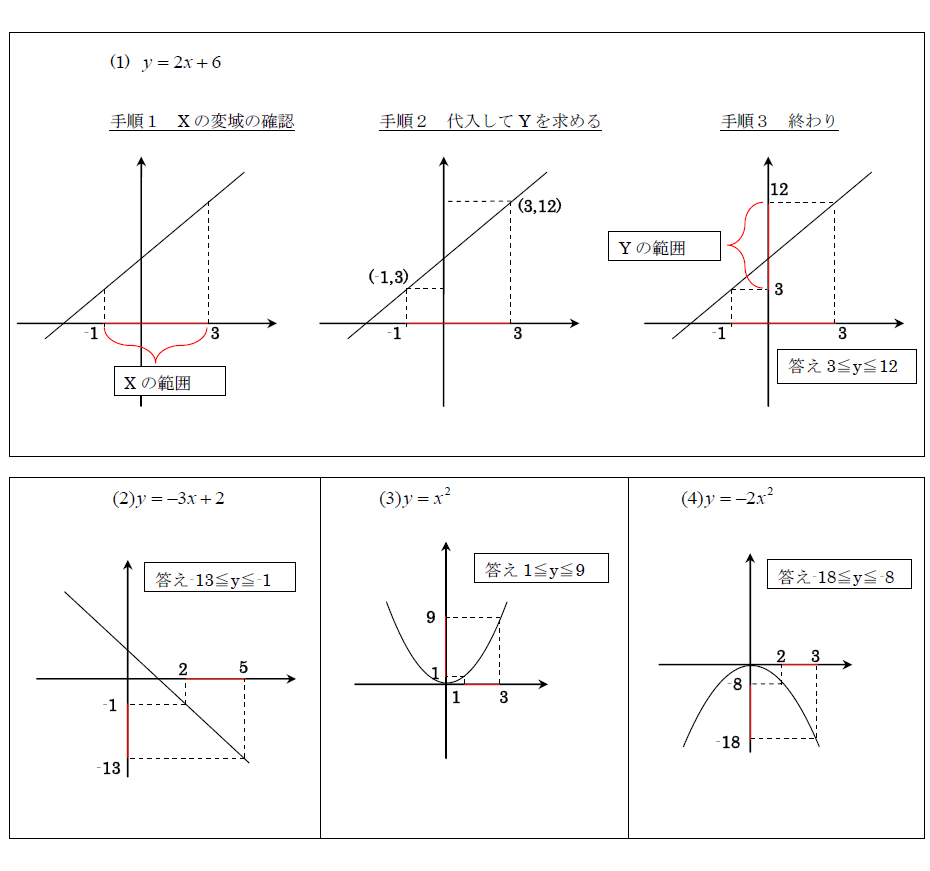
受験 定期試験 数学解き方集 裏技 解法 １次関数 ２次関数の変域 中学数学

切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ

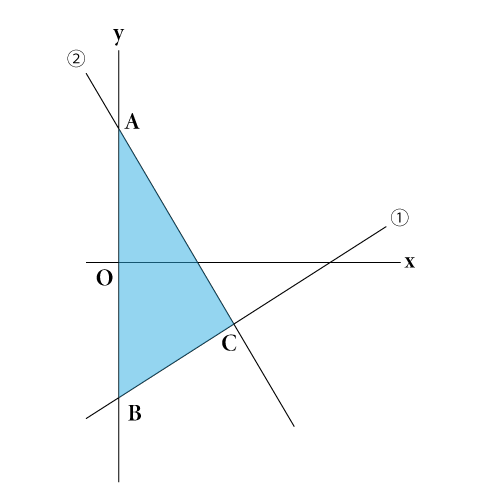
中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾

一次関数のグラフ 無料で使える中学学習プリント

Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ The 2nd

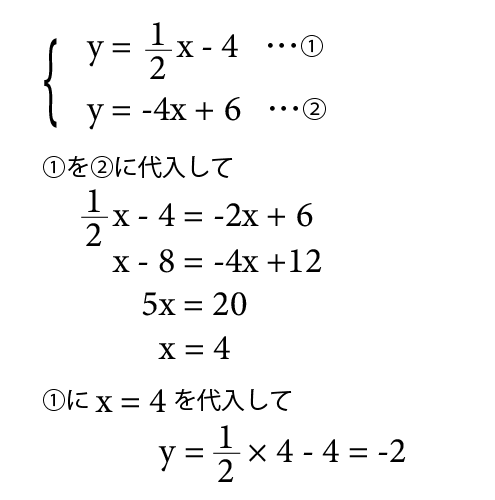
中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾

お勉強 図形問題で一次関数 解き方のご提案 そらの暇つぶしch

１次関数の値の変化 増加量と変化の割合 教遊者

Incoming Term: 1次関数 解き方, １次関数 解き方, 1次関数 解き方 中学,